Down sampling more
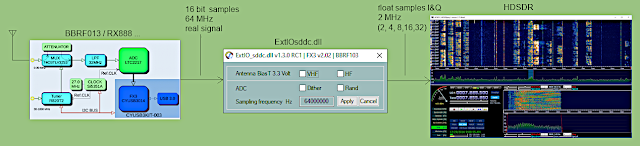
ExtIO_sddc.dll is designed for use of BBRF103 / RX888 with HDSDR.
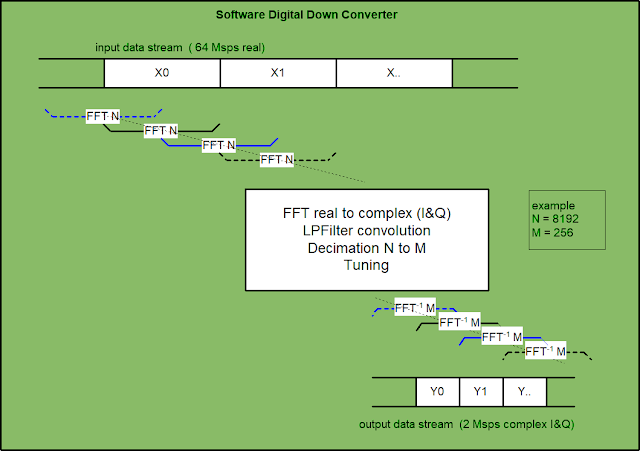
The input stream from the ADC ( 16bit , 64 MHz real signal) is analyzed in an overlap and save method (overlap-scrap) with an FFT of dimension N = 8192 .
After the low pass filtering convolution an output FFT-1 of dimension M = 256 decimates the sampling rate to 2 MHz .
64 * 256 / 8192 = 2 MHz.
Signal tuning is made with circular shift in frequency and fine tuning using a complex mixer in time.
This is a simplified diagram of SDDC:
If we want to use a stand alone application deeper decimation and filtering is required to match the computer audio sampling.
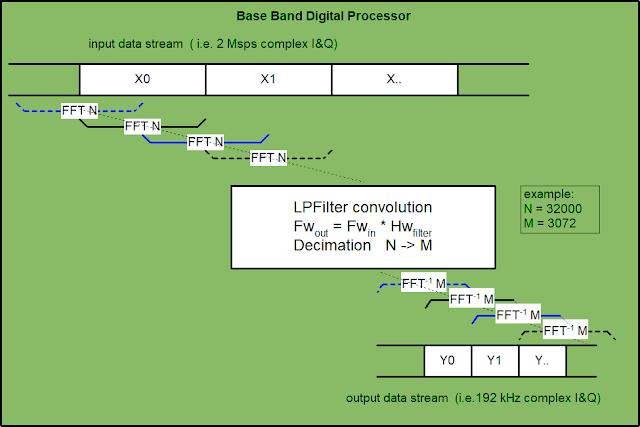
A possible block diagram of the application is:
The Base Band Digital Processor module receives an I&Q input at 2 MHz and generates an output to demodulation module at "audio" speed..
Here some numbers.
/*
F INPUT FFT FFT F OUT
(kHz) (N) (M) (kHz)
2000 32000 192 12
2000 32000 384 24
2000 32000 768 48
2000 32000 1536 96
2000 32000 3072 192
2000 32000 6144 384
2000 32000 12288 768
2000 32000 24576 1536
2000 32381 714 44,09997
*/
Suppose you want to produce a 192 kHz output stream at the demodulation block from a sampling rate of 2 MHz.
You can use an FFT of 32000 samples of the input stream and apply an overlap-scrap pattern low-pass filter with a cutoff frequency close to 90 kHz.
The output time frequency is decimated with an FFT-1 of 3072 samples with a result time rate:
2000 * 3072 / 32000 = 192 kHz
The prime factorization of the FFT dimensions are:
32000 = 28 x 53 ,
3072 = 210 x 3 ,
While 32381 is a prime number and it rises computing complexity.
It is simpler to stay on the 12 kHz harmonics audio sampling rates.
It seems convenient to keep the size of the first FFT in SDDC small to be fast but large enough to allow implementation of a sufficient bandpass filter and use a longer FFT at a lower sampling rate to model the final demodulation selectivity in the BBDP module.
I made a rough estimate. Suppose we have 65536 samples and FFT complexity 𝑂(N𝑙𝑜𝑔2(N)).
We process them with an FFT of 8192 points by dividing them into segments of FFT length.
The total complexity will be order of ( 65536 / 8192) * 8192 *𝑙𝑜𝑔2 (8192) = 65536 * 13;
With FFT length 32768 we get (65536 / 32768)* 32768 *𝑙𝑜𝑔2(32768) = 65536 * 15 ;
At this development stage I prefer to test the BBDP module with FFT 32000 separate from the SDDC one that uses FFT 8192 .The latency at 2 MHz of 32000 FFT frame is 16 ms.
A draft code console prototype without the GUI is my preview toy.
..continue.



Comments
Post a Comment